
|
Number & Computation A
Years 2 - 6(8)
|

|
A Mathematics Centre Resource

You are encouraged to contribute to these notes. Comments from teachers or students, photos and student work samples will enrich the professional experience for all of us.
Menu
Introduction
Print Resources
|
 |
Materials
- Poly Plug
(from Mathematics Centre)
- See Equipment List for source of Poly Plug or substitute equipment if necessary.
|
 |

|
Picture Puzzles have multiple levels of success. They do not have to be 'finished'. They can be revisited and continued.

In the context of working like a mathematician, the focus of all the Picture Puzzles in this menu is on 'ways of knowing' by strongly encouraging the question Can I check this another way?. We do want learners to be automatic with their times tables responses, but to be so from the basis of a secure, flexible conceptual understanding. These Puzzles are one step towards that objective.
This menu of Picture Puzzles is based on Uncover Counting from Calculating Changes (which requires separate membership).

|
Summary
Students use their Poly Plug to create their own six times table array of blue plugs. Then they cover the array and reveal it row by row first predicting, then calculating in several ways, the total number of plugs that can be seen. This explores the six times table up to 5 x 6. This information is then built on as the students imagine the array extended to 10 rows of 6 blue plugs and have to calculate, again in many ways, the times tables up to 10 x 6.
Additional challenges include what happens if questions related to alternative, but equivalent, arrays and working backwards to find the number of rows if you know the number of plugs. One final challenge involves finding, given certain information, the number of plugs still covered.
|
Answers
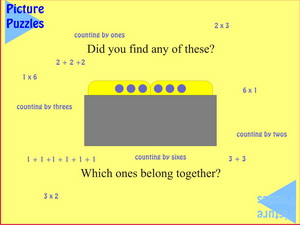
|
Before reaching this slide students have been asked to find 5 ways to know that there are six blue plugs showing. The slide is intended to confirm their chosen ways and suggest that there are other ways. The question of belonging together could be answered in more than one way, so students should be encouraged to record the reason(s) for their categories. One answer could be: I did it like this because I like the pattern.
| Counting by ones |
Counting by twos |
Counting by threes |
Counting by sixes |
| 1 + 1 + 1 + 1 + 1 + 1 |
2 + 2 + 2 |
3 + 3 |
6 |
| 6 x 1 |
3 x 2 |
2 x 3 |
1 x 6 |
|
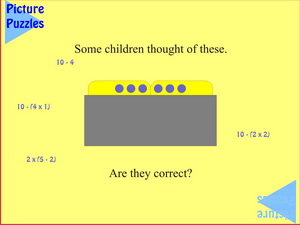
|
One of the advantages of Poly Plug is that the complement (in this case to 10) is always present. This encourages students to see the subtractive ways of knowing that there are six blue plugs showing. When challenged to explain expressions like these they often press up the yellow ones at the end of the row, say something like See there are ten. Now I take away... and then slap down the ones being subtracted.
The other advantage of Poly Plug is that the boards are 5x5, which is why students soon start to see that the partition can be used to create expressions such as 2x(5 - 2) = 6.
|
Of course, this slide is also included to validate that such creative thinking is valued. So, even if your students haven't thought of these alternatives, they recognise that's it's now okay for them 'think out of the box' and begin to do so in the next set of challenges.
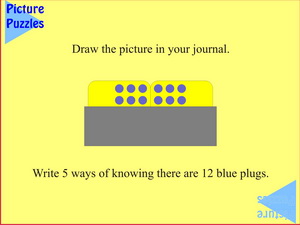

|
This arrangement encourages counting by ones, twos, threes, fours and sixes and the plugs can be touched with finger tips to show what is meant. Then there are the additive and multiplicative versions of this counting as well as the complement of ten versions that involve multiples of 1, 2 and 4 - or if students get really 'tricky', multiples of 3 with multiples of 1. The complement this time is from 20, or it could be multiples from 10 or 5. So, all up there are many more than ten possible ways of knowing.
If students seem a bit stuck in the additive ones such as 2 + 2 + 2 + 2 + 2 + 2 = 12 ask:
- Can you read this to me?
- How many times did you say 2?
- So, six times two equals?
- How would you write that on your calculator?
|
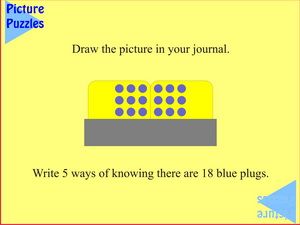

|
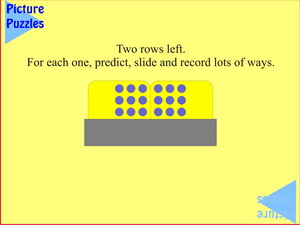
Three rows of six suggests counting by ones, twos, threes, sixes (in more than one way) and nines (often subitised from the Channel 9 symbol), with all the attendant variations, including the complements.
What's the most number of ways you can find to know that 18 blue plugs are showing?
|
|
Here it is assumed that the students now understand the structure of the slides and it becomes a 'game' of searching for the most ways they can find.
Remember, you don't have to correct their work. They have to convince a colleague that any recording is correct.
|
|
And here the game continues, but the visual aid has to be imagined.
(If necessary, this where the Poly Plug Recording Grid might be useful for some students to help bridge from the concrete.)
|

|
Prior to this slide the students have been asked to make their prediction and check it another way. This slide is provided as a visual basis for checking their reasoning. What matters is that they are able to articulate (and hence record in words and/or drawings) their two ways of calculating the number of rows given the number of plugs.
|


|
These slides imply the question:
- What happens if the array had been differently presented? Would you have calculated in a different way?
To some extent it matters more here that students realise that for a mathematician there is always a new question to ask, rather than what they actually answer about the calculation alternative.
The next set of challenges is a repeat of these with 54 plugs in rows of six.
|

|
This final challenge opens the door to many similar questions. We first need to calculate the number of rows for the (comparatively large) given number of plugs. Then subtract seven rows of 'seen' plugs to find the number of rows of hidden plugs. Then we have to work out 18 rows of 6 = 18 x 6, which can be done by combining two of the previously obtained results.
Or is there another way?
|


|
Summary
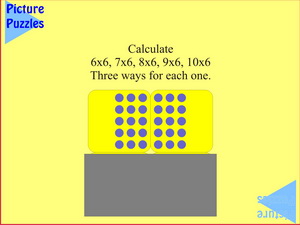
Students use their Poly Plug to create their own seven times table array of blue plugs. Then they cover the array and reveal it row by row first predicting, then calculating in several ways, the total number of plugs that can be seen. This explores the seven times table up to 5 x 7. This information is then built on as the students imagine the array extended to 10 rows of 7 blue plugs and have to calculate, again in many ways, the times tables up to 10 x 7.
Additional challenges include what happens if questions related to an alternative, but equivalent, array and working backwards to find the number of rows if you know the number of plugs. One final challenge involves finding, given certain information, the number of plugs still covered.
|
Answers

|
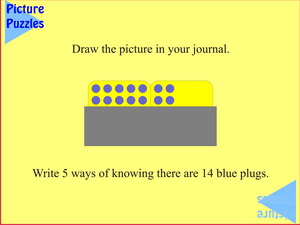
Before reaching this slide students have been asked to find 5 ways to know that there are six blue plugs showing. The slide is intended to confirm their chosen ways and suggest that there are other ways. The question of belonging together could be answered in more than one way, so students should be encouraged to record the reason(s) for their categories. One answer could be:
| Counting by ones |
Counting by twos + one |
Counting by threes + one |
Counting by sevens |
| 1 + 1 + 1 + 1 + 1 + 1 |
2 + 2 + 2 + 1 |
3 + 3 + 1 |
7 |
| 7 x 1 |
3 x 2 +1 |
2 x 3 + 1 |
1 x 7 |
5 + 2 comes into its own as more rows are revealed, but at the moment it might also be (1 x 5) + (1 x 2) and the brackets correspond to the separate Poly Plug boards.
|

|
One of the advantages of Poly Plug is that the complement (in this case to 10) is always present. This encourages students to see the subtractive ways of knowing that there are seven blue plugs showing. When challenged to explain expressions like these they often press up the yellow ones at the end of the row, say something like See there are ten. Now I take away... and then slap down the ones being subtracted.
The other advantage of Poly Plug is that the boards are 5x5, which is why students soon start to see that the partition can be used to create expressions such as 5 + (5 - 3) = 7, or 2 x 5 - 3 = 7.
|
Of course, this slide is also included to validate that such creative thinking is valued. So, even if your students haven't thought of these alternatives, they recognise that's it's now okay for them 'think out of the box' and begin to do so in the next set of challenges.

|
In this arrangement students will readily see counting by ones, twos and sevens and might include counting by threes with the extra ones, but they might also include counting by fours with an extra two. The plugs can be touched with finger tips to show what is meant. However, what is much more obvious now is breaking 7 into its 5 and 2 parts. So 14 is fourteen because it is made up of two sevens which means 2 x 5 + 2 x 2.
Then there are the additive and multiplicative versions of the counts above as well as the complement of ten versions that involve multiples of 1, 2, 3 and 6. The complement this time is from 20, or it could be multiples from 10 or 5. So, all up there are many more than ten possible ways of knowing.
If students seem a bit stuck in the additive ones such as 2 + 2 + 2 + 2 + 2 + 2 + 2= 14 ask:
- Can you read this to me?
- How many times did you say 2?
- So, seven times two equals?
- How would you write that on your calculator?
|

|
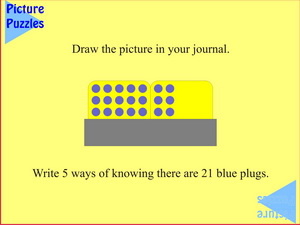
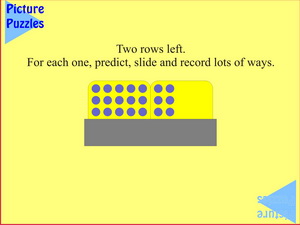
Three rows of seven suggests counting by ones, threes and sevens with all the attendant variations, including the complements. But again the 5/2 split is made obvious by the boards, hence 3 x 5 + 3 x 2 = 21 is quite natural too.
What's the most number of ways you can find to know that 21 blue plugs are showing?
|
|
Here it is assumed that the students now understand the structure of the slides and it becomes a 'game' of searching for the most ways they can find.
Remember, you don't have to correct their work. They have to convince a colleague that any recording is correct.
|
|
And here the game continues, but the visual aid has to be imagined.
(If necessary, this where the Poly Plug Recording Grid might be useful for some students to help bridge from the concrete.)
|

|
Prior to this slide the students have been asked to make their prediction and check it another way. This slide is provided as a visual basis for checking their reasoning. What matters is that they are able to articulate (and hence record in words and/or drawings) their two ways of calculating the number of rows given the number of plugs.
|

|
This slide implies the question:
- What happens if the array had been differently presented? Would you have calculated in a different way?
To some extent it matters more here that students realise that for a mathematician there is always a new question to ask, rather than what they actually answer about the calculation alternative.
The next set of challenges is a repeat of these with 56 plugs in rows of six.
|

|
This final challenge opens the door to many similar questions. We first need to calculate the number of rows for the (comparatively large) given number of plugs. Then subtract seven rows of 'seen' plugs to find the number of rows of hidden plugs. Then we have to work out 18 rows of 7 = 18 x 7, which can be done by combining two of the previously obtained results.
Or is there another way?
|


|
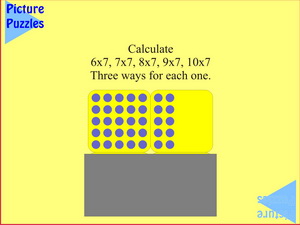
Summary
Students use their Poly Plug to create their own eight times table array of blue plugs. Then they cover the array and reveal it row by row first predicting, then calculating in several ways, the total number of plugs that can be seen. This explores the eight times table up to 5 x 8. This information is then built on as the students imagine the array extended to 10 rows of 8 blue plugs and have to calculate, again in many ways, the times tables up to 10 x 8.
Additional challenges include what happens if questions related to an alternative, but equivalent, array and working backwards to find the number of rows if you know the number of plugs. One final challenge involves finding, given certain information, the number of plugs still covered.
|
Answers
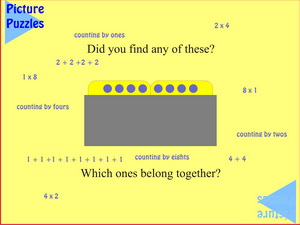
|
Before reaching this slide students have been asked to find 5 ways to know that there are eight blue plugs showing. The slide is intended to confirm their chosen ways and suggest that there are other ways. The question of belonging together could be answered in more than one way, so students should be encouraged to record the reason(s) for their categories. One answer could be:
| Counting by ones |
Counting by twos |
Counting by fours |
Counting by eights |
| 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 |
2 + 2 + 2 + 2 |
4 + 4 |
8 |
| 8 x 1 |
4 x 2 |
2 x 4 |
1 x 8 |
|

|
One of the advantages of Poly Plug is that the complement (in this case to 10) is always present. This encourages students to see the subtractive ways of knowing that there are eight blue plugs showing. When challenged to explain expressions like these they often press up the yellow ones at the end of the row, say something like See there are ten. Now I take away... and then slap down the ones being subtracted.
The other advantage of Poly Plug is that the boards are 5x5, which is why students soon start to see that the partition can be used to create expressions such as 2x(5 - 1) = 8.
|
Of course, this slide is also included to validate that such creative thinking is valued. So, even if your students haven't thought of these alternatives, they recognise that's it's now okay for them 'think out of the box' and begin to do so in the next set of challenges.
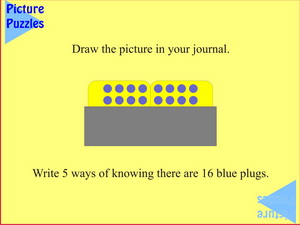

|
This arrangement encourages counting by ones, twos (in two ways), fours (in two ways) and eights and the plugs can be touched with finger tips to show what is meant. Then there are the additive and multiplicative versions of this counting as well as the complement of ten versions that involve multiples of 1, 2 and 4. The complement this time is from 20, or it could be multiples from 10 or 5. So, all up there are many more than ten possible ways of knowing.
If students seem a bit stuck in the additive ones such as 4 + 4 + 4 + 4 = 16 ask:
- Can you read this to me?
- How many times did you say 4?
- So, four times four equals?
- How would you write that on your calculator?
|
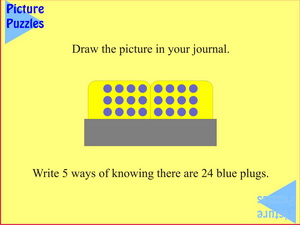

|
Three rows of eight suggests counting by ones, twos, threes, fours, sixes, eights and even twelves, with all the attendant variations, including the complements. Factors of 24 are now very clear.
What's the most number of ways you can find to know that 24 blue plugs are showing?
|
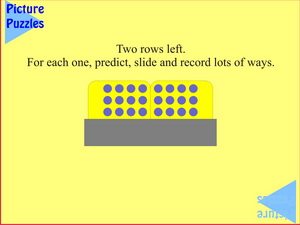
|
Here it is assumed that the students now understand the structure of the slides and it becomes a 'game' of searching for the most ways they can find.
Remember, you don't have to correct their work. They have to convince a colleague that any recording is correct.
|
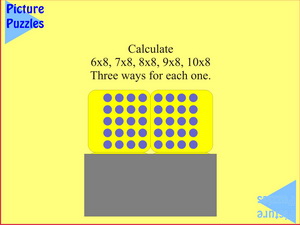
|
And here the game continues, but the visual aid has to be imagined.
(If necessary, this where the Poly Plug Recording Grid might be useful for some students to help bridge from the concrete.)
|

|
Prior to this slide the students have been asked to make their prediction and check it another way. This slide is provided as a visual basis for checking their reasoning. What matters is that they are able to articulate (and hence record in words and/or drawings) their two ways of calculating the number of rows given the number of plugs.
|

|
This slide implies the question:
- What happens if the array had been differently presented? Would you have calculated in a different way?
To some extent it matters more here that students realise that for a mathematician there is always a new question to ask, rather than what they actually answer about the calculation alternative.
However, the 5/3 split can be very powerful since:
7 rows of 8 = 7 x 8 = 7 x (5 + 3) = 7 x 5 + 7 x 3
is a particular example of the Distributive Law and the split between the boards makes the mathematics seem natural.
The next set of challenges is a repeat of these with 72 plugs in rows of eight.
|

|
This final challenge opens the door to many similar questions. We first need to calculate the number of rows for the (comparatively large) given number of plugs. Then subtract seven rows of 'seen' plugs to find the number of rows of hidden plugs. Then we have to work out 18 rows of 8 = 18 x 8, which can be done by combining two of the previously obtained results.
Or is there another way?
|


|
Summary
Students use their Poly Plug to create their own nine times table array of blue plugs. Then they cover the array and reveal it row by row first predicting, then calculating in several ways, the total number of plugs that can be seen. This explores the nine times table up to 5 x 9. This information is then built on as the students imagine the array extended to 10 rows of 9 blue plugs and have to calculate, again in many ways, the times tables up to 10 x 9.
Additional challenges include seeing the nine times table as one less than the tens and working backwards to find the number of rows if you know the number of plugs. One final challenge involves finding, given certain information, the number of plugs still covered.
|
Answers
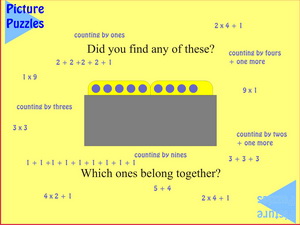
|
Before reaching this slide students have been asked to find 5 ways to know that there are six blue plugs showing. The slide is intended to confirm their chosen ways and suggest that there are other ways. The question of belonging together could be answered in more than one way, so students should be encouraged to record the reason(s) for their categories. One answer could be:
| Counting by ones |
Counting by twos + one |
Counting by threes |
Counting by fours + 1 |
Counting by nines |
| 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 |
2 + 2 + 2 + 2+ 1 |
3 + 3 + 3 |
4 + 4 + 1 |
9 |
| 9 x 1 |
4 x 2 +1 |
3 x 3 |
2 x 4 + 1 |
1 x 9 |
5 + 4 comes into its own as more rows are revealed, but at the moment it might also be (1 x 5) + (1 x 4) or (1 x 5) + (2 x 2) and the brackets correspond to the separate Poly Plug boards.
|

|
One of the advantages of Poly Plug is that the complement (in this case to 10) is always present. This encourages students to see the subtractive ways of knowing that there are nine blue plugs showing. When challenged to explain expressions like these they often press up the yellow one at the end of the row, say something like See there are ten. Now I take away... and then slap down the one being subtracted.
The other advantage of Poly Plug is that the boards are 5x5, which is why students soon start to see that the partition can be used to create expressions such as 5 + (5 - 1) = 9, or 2 x 5 - 1 = 9.
|
Of course, this slide is also included to validate that such creative thinking is valued. So, even if your students haven't thought of these alternatives, they recognise that's it's now okay for them 'think out of the box' and begin to do so in the next set of challenges.
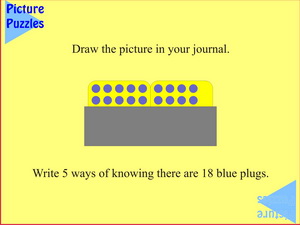

|
In this arrangement students will readily see counting by ones, twos, threes and nines and might include counting by fours with the extra ones. The plugs can be touched with finger tips to show what is meant. However, what is much more obvious now is breaking 9 into its 5 and 4 parts. So 18 is eighteen because it is made up of two nines which means 2 x 5 + 2 x 4 (and the fours can be seen in two ways).
Then there are the additive and multiplicative versions of the counts above as well as the complement of ten versions that involve multiples of 1 and 2. The complement this time is from 20, or it could be multiples from 10 or 5. So, all up there are many more than ten possible ways of knowing.
If students seem a bit stuck in the additive ones such as 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 18 ask:
- Can you read this to me?
- How many times did you say 2?
- So, nine times two equals?
- How would you write that on your calculator?
|
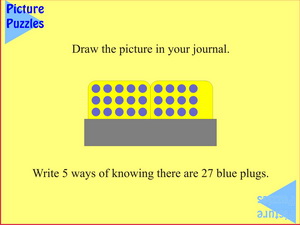

|
Three rows of nine suggests counting by ones, threes (in two ways) and nines with all the attendant variations, including the complements. But again the 5/4 split is made obvious by the boards, hence 3 x 5 + 3 x 4 = 27 is quite natural too.
What's the most number of ways you can find to know that 27 blue plugs are showing?
|
|
Here it is assumed that the students now understand the structure of the slides and it becomes a 'game' of searching for the most ways they can find.
Remember, you don't have to correct their work. They have to convince a colleague that any recording is correct.
|
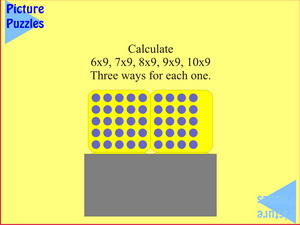
|
And here the game continues, but the visual aid has to be imagined.
(If necessary, this where the Poly Plug Recording Grid might be useful for some students to help bridge from the concrete.)
|

|
Prior to this slide the students have been asked to make their prediction and check it another way. This slide is provided as a visual basis for checking their reasoning. What matters is that they are able to articulate (and hence record in words and/or drawings) their two ways of calculating the number of rows given the number of plugs.
|

|
This final challenge opens the door to many similar questions. We first need to calculate the number of rows for the (comparatively large) given number of plugs. Then subtract seven rows of 'seen' plugs to find the number of rows of hidden plugs. Then we have to work out 18 rows of 9 = 18 x 9, which can be done by combining two of the previously obtained results.
Or is there another way?
|


|
Summary
Students use their Poly Plug to create their own ten times table array of blue plugs. Then they cover the array and reveal it row by row first predicting, then calculating in several ways, the total number of plugs that can be seen. This explores the ten times table up to 5 x 10. This information is then built on as the students imagine the array extended to 10 rows of 10 blue plugs and have to calculate, again in many ways, the times tables up to 10 x 10.
Additional challenges include what happens if questions related to working backwards to find the number of rows if you know the number of plugs. One final challenge involves finding, given certain information, the number of plugs still covered.
|
One thing students are likely to realise, especially if they have tried some of the other puzzles on the menu first, is that there seem to be fewer ways to calculate the 10 times table. Good thing it's easier to learn.
Answers

|
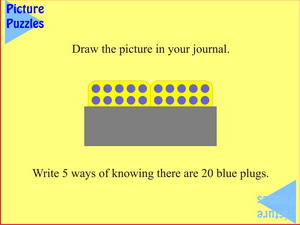
Before reaching this slide students have been asked to find 5 ways to know that there are ten blue plugs showing. The slide is intended to confirm their chosen ways and suggest that there are other ways. The question of belonging together could be answered in more than one way, so students should be encouraged to record the reason(s) for their categories. One answer could be:
| Counting by ones |
Counting by twos |
Counting by fives |
Counting by tens |
| 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 |
2 + 2 + 2 + 2 + 2 |
5 + 5 |
10 |
| 10 x 1 |
5 x 2 |
2 x 5 |
1 x 10 |
|

|
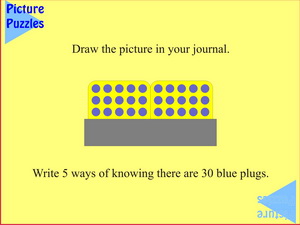
This arrangement encourages counting by ones, twos (in two ways), fours, fives and tens and the plugs can be touched with finger tips to show what is meant. Then there are the additive and multiplicative versions of this counting.
If students have tried other puzzles from this menu before this one, they may notice that complement to ten calculations can't be made in this case. Again, perhaps this is why the tens table is easier to learn.
If students seem a bit stuck in the additive alternatives such as 4 + 4 + 4 + 4 + 4 = 20 ask:
- Can you read this to me?
- How many times did you say 4?
- So, five times four equals?
- How would you write that on your calculator?
|
|
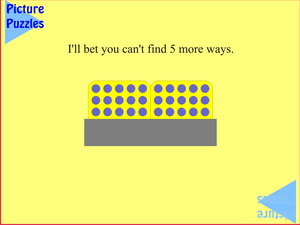
Three rows of ten suggests counting by ones, twos, threes, fives, sixes, tens and even fifteens, with all the attendant variations. Factors of 30 are now very clear.
What's the most number of ways you can find to know that 30 blue plugs are showing?
|
|
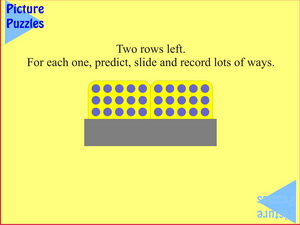
Here it is assumed that the students now understand the structure of the slides and it becomes a 'game' of searching for the most ways they can find.
Remember, you don't have to correct their work. They have to convince a colleague that any recording is correct.
|
|
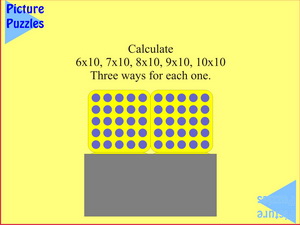
And here the game continues, but the visual aid has to be imagined.
(If necessary, this where the Poly Plug Recording Grid might be useful for some students to help bridge from the concrete.)
|

|
Prior to this slide the students have been asked to make their prediction and check it another way. This slide is provided as a visual basis for checking their reasoning. What matters is that they are able to articulate (and hence record in words and/or drawings) their two ways of calculating the number of rows given the number of plugs.
The next set of challenges is a repeat with 90 plugs in rows of ten. |

|
This final challenge opens the door to many similar questions. We first need to calculate the number of rows for the (comparatively large) given number of plugs. Then subtract seven rows of 'seen' plugs to find the number of rows of hidden plugs. Then we have to work out 18 rows of 10 = 18 x 10, which can be done by combining two of the previously obtained results.
Or is there another way?
|

|





























































