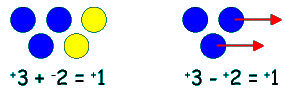|
Introducing Algebra

Years 6 - 8 |
Summary
The idea of each plug having a value - usually 1 - is built into almost all of the Calculating Changes activities. In this activity that idea is extended based on learning from Task 130, Protons & Anti-Protons, in which each blue plug is worth positive 1 (+1)and each yellow plug is worth negative one (-1). Therefore any collection of equal numbers of blue and yellow plugs is worth zero.
But can we use the red plugs be for anything?
Well, they could represent the value of a mystery collection of yellow and blue plugs. Aha! Now we can represent algebraic expressions and equations and explore that 'text book stuff' in a visual, concrete way. Suitable for threading.
Materials
- One Poly Plug set per pair
Acknowledgement
This activity was contributed by Tony Wright, Bellarine Secondary College.
|

|
Preparation
This activity builds on experience with Protons & Anti-Protons from the Mathematics Task Centre. In this task, a plug blue side up represents +1 and a plug yellow side up represents -1. The task also introduces two key concepts of integer arithmetic which become the basis of this Introducing Algebra activity.
- Any positive or negative number can be represented by an infinite number of collections. For example, each of the three collections shown is worth 3 Protons (or +3) because equal numbers of positive and negative units in any collection sum to zero.
|

|
- Adding a negative gives the same answer as subtracting a positive.
(There is an extra refinement here. By convention, mathematicians agree that, to save a bit of writing, a positive number doesn't have to have the positive sign. In other words, if a number doesn't have a sign, assume it is positive. That means the two equations in the picture could be written as:
3 + -2 = 1 and 3 - 2 = 1)
|
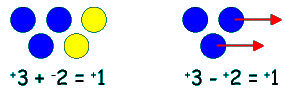
|
|
|
Content
- algebra, equivalent expressions
- algebra, factorisation
- algebra, like & unlike terms
- algebra, linear
- conservation of number
- equations: creating/solving
- multiplication - array model
- negative numbers
- order of operations
- problem solving
- properties of number
- properties of zero
- recording - written
- using brackets
- visual and kinaesthetic representation of number
|
Procedure
Now, if we know what a number is, we can make it. We can also represent it with any collection that suits our problem at the time. But what happens if we don't know what the number is, for example, if someone has put some plugs in a box?
Well, we could represent the unknown number in the box by drawing the box, or by using something, say a red plug, to stand for it. Then we could try to find out more about how the value in the box combines with numbers we do know.
In this approach, algebraic representation becomes just another What happens if...? adventure of that mathematicians love to play with.
The procedure is to explore as a threaded activity - a little bit often - to help the children grow confident with their manipulation and recording of algebraic expressions. Not because algebraic manipulation is the main objective, but because the challenges explored are interesting and a mathematician's work begins with an interesting problem and data gathered in the investigation of it needs to be recorded.
What are the learning features of this activity likely to make it interesting for children?
Algebraic Expressions
Preparation activities such as these grow confidence in representing any particular positive or negative number. For example:
- Make a collection of yellow and blue plugs with a value of -7.
- Make the same value another way.
- Make the same value so it includes exactly three -1 plugs.
- Make and record 5 different collections with a value of -7.
The journal record for these would be several pictures, but even though the pictures would look different the value of each picture would be the number -7. This is the symbolic representation of each picture.
But how do we record the value of a hidden number of plugs if it is being represented by a red plug? Well, as long as we don't actually use a number, it doesn't matter what we choose. We could draw a box, but mathematicians usually choose a letter of the alphabet. So,
(Editor's Note: How about r or R? You might think this is better because it is a more natural replacement for a red plug.)
Now we can make all sorts of collections that include red plugs, remembering that.
- The red plug represents the value of a box with an unknown number of yellow and blue plugs, and
- If there is more than one red plug in the same problem, each one represents the same value.
For example:
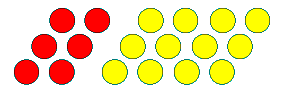
The value of 6 red plugs (6 mystery boxes with the same collection inside) would be 6x.
Then this collection represents 6x - 12 because adding the negative has the same effect as subtracting the positive.
Make this collection and record how you can sort it into equal groups to represent:
|
|
- 3(2x - 4) meaning 3 rows of (2x - 4)
- 6(x - 2) meaning 6 rows of (x - 2)
- 2(3x - 6) meaning 2 rows of (3x - 6)
That's what factorising is all about. Finding ways to make a total collection into rectangles.
Expanding is asking the reverse question, for example:
We have 5 rows of (x plus 1), ie: 5(x + 1). Make them then write the total a different way.
Isn't this more fun and more meaningful than drill and kill exercises from a text book?
Linear Equations
Now suppose the person who hid the plugs in the box still doesn't tell us the total value of the collection in the box, but does give us a clue.
For example, suppose we are told that 5(value in the box) - 6 = 4.
Our challenge is to find the value of the plugs hidden in the box.
This value is represented by a red plug when we make a model and draw a picture of the equation and by x when we record it in symbols.
So, what is the value of x if 5x - 6 = 4?
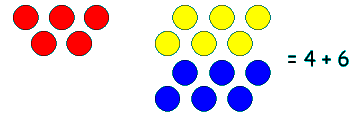
- Keep it equal by doing the same thing to both sides. In this case adding a number that makes the total collection of known plugs zero. Then all the value on the right hand side must come from the red plugs...
|
|
- So five things with the same value are worth 10, so we can work out the value of each thing (red plug, mystery box)...
|

|
- And we get the answer x = 2...
- Substitute that value back into the original collection to check that it works.
|

|
So, the person hid plugs with a value of 2 inside the mystery box.
(Editor's Note: However what we still don't know - and it doesn't matter - is which of the infinite ways of representing 2 was actually inside the box.)
As with the algebraic expressions section above, children tackling one or two of these equation solving challenges a day (perhaps at a work station), sometimes invented by the teacher, sometimes invented by the children, for three or four days each week over two or three weeks, leads to more involvement, more understanding and more confidence with tackling text-type questions.
- What happens if the clue is a bit trickier and has x (the mystery box value) on both sides, eg: 3x + 7 = 22 - 2x?
Extensions
- Other 'mystery box' activities that lead into or complement this activity are Number Shapes and Trial, Record & Improve (both Free Tour) and the Member activities Box Hunt, Six Plus and What's My Rule?.
- Maths300 members could enrich the activity with Lesson 19, Backtracking, Lesson 34, What's My Rule?, Lesson 84, Number Charts, Lesson 94, Trial, Record & Improve, Lesson 156, Chart Strategies, and Lesson 160, Algebra Charts.

Calculating Changes ... is a division of ... Mathematics Centre
|