
|
Making & Breaking Rectangles
Years 2 - 7
|

Preparation
Turn off your sound, then click the image to watch this 2min 32sec video with someone else.
 TURN OFF YOUR SOUND FIRST TURN OFF YOUR SOUND FIRST
- Together, make a list of the things you saw.
- Watch the video again without sound to see if you want to add to your list.
Explaining The Video
Talk with each other to answer these questions in your journal:
- The person in the background was using 24 bottle tops. What was she doing with them?
- When the third person came into the picture he had 24 bottle tops too? What was he doing with them?
- Suppose you had 24 bottle tops.
- What other number could you choose that would work?
- What other number could you choose that would not work?
- What number of bottle tops could you choose so that rows of five (5) would work?
Turn on your sound and watch the video again.
- Do you want to add anything to your journal notes about the video?
 |
 |
|
Before you continue with this activity you need to collect 30 or more objects all the same - bottle tops, plastic screw caps, buttons, pebbles from the garden, pasta.
They have to be small enough to make rows on your work table.
|
 |
Learning About Rows
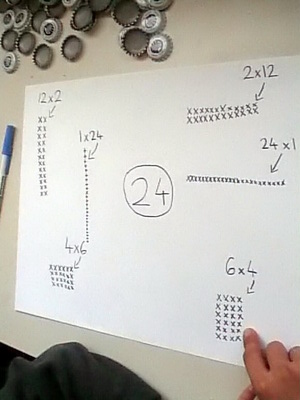 |
The person is pointing to a picture of 24 arranged in equal rows.
- Rows go across your tummy.
- It's like when an actor stands on stage and the audience are sitting in rows
... across the actor's tummy.
- Equal rows make a rectangle shape.
How many rows in the picture? Six (6).
How many objects in each row? Four (4).
- 24 makes 6 rows of 4.
- If you run your finger across each row you touch 4 each time.
- That's 6 times you touch 4.
- 24 = 6 times 4
- Some mathematicians use x to stand for rows of or times.
- These three things mean the same:
24 = 6 rows of 4
24 = 6 times 4
24 = 6 x 4
All the pictures on this sheet are correct.
But check the 'times' for each one. Two (2) of them are not correct.
- Draw the two in your journal and write the correct 'rows of' and 'times' for each of them.
There are two more ways to make 24 into equal rows.
- Draw them and write the 'rows of' and the 'times' for each.
|
Making & Breaking Your Own Rectangles
Now it's your turn to choose a number and find all the ways it makes equal rows.
- You can use your calculator to help if you want to.
- Record a drawing and the 'rows of' and 'times' for each way you find.
Have fun Making & Breaking Rectangles.
We suggest you do 2 or 3 numbers a day for 2 or 3 days each week for the next 2 or 3 weeks.
Special Rectangles
Prime Numbers can only make rectangles in two ways. They are: 1 row of ... and ... rows of 1.
- Write the smallest Prime Number.
- Find a Prime Number bigger than 40.
Square Numbers have a square as one of the rectangles they make.
- Write the smallest Square Number.
- Find a Square Number bigger than 50.
Factors are all the numbers used to make all the rectangles of a number. But you only write each number once.
- The children in the video found these factors of 24 ... 1, 2, 4, 6, 12, 24, but they didn't find 3 and 8.
- The complete set of factors for 24 is (1, 2, 3, 4, 6, 8, 12, 24). Twenty-four (24) has eight (8) factors.
- Go back through the numbers in your journal and write the set of factors for each number.
Note: If your school is a member of Maths300, your teacher can provide software, titled Tackling Time Tables, that will help you investigate this activity.
Rectangles On Paper
- Print this sheet of Rectangles for 20 and follow the instructions.
- On a page in your journal, arrange the rectangles so the bottom left corners are on top of each other like the ones in this picture.
- Stick them down.
- Put a dot on the top right corner of each rectangle write the 'times' for that rectangle near it.
- Beside the picture write the factors of 20.
- Turn the book so your hand is inside the picture pointing towards the corner where the rectangles join. With a pencil, try to join the dots with a smooth curve. This curve is called a hyperbola.
Print this Square Line Paper and draw all the rectangles for one of the numbers less than 20 with the most factors.
- Repeat the experiment for your rectangles.
- Record anything you notice in your journal.
|
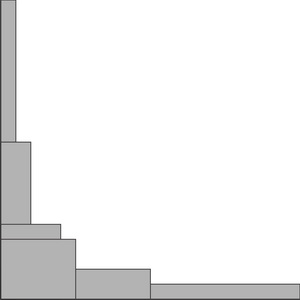 |
Extra Challenge: More About The Hyperbola
The hyperbola for 20 shows you all the factors of 20 and every pair of numbers that multiply together to equal 20.
Challenge
Use your calculator to help you find the number of rows of 4·5 to make 20.
- That is you need to find the missing number in ... x 4·5 = 20
Just Before You Finish
For this part you need your maths journal and your Working Like A Mathematician page.
- Read again what it means to work like a mathematician.
- In your journal, finish this paragraph:
Working with Making & Breaking Rectangles I was a successful mathematician because...
- Explain any maths you think you will be better at now because you tried this activity.

Answers & Discussion
These notes were originally written for teachers. They have been adapted and shared from the Members section of Calculating Changes, which is a division of Mathematics Centre. If you need more explanation of anything in this activity you can send an email to doug@blackdouglas.com.au.
Send any comments or photos about this activity and we can start a gallery here.

Maths At Home is a division of Mathematics Centre
|






