
|
Truth Tiles 2
Years 2 - 10
|

Preparation
- Fold a piece a piece of A4 paper in half three (3) times to make eight (8) sections.
- Cut out all eight pieces.
- Choose five (5) and write the numbers 3, 4, 5, 6, 7 - one (1) big number on each piece.
- Write one of these symbols ... +, -, = ... on each of the other three pieces
- Write the title of this challenge and today's date on a fresh page in your maths journal.
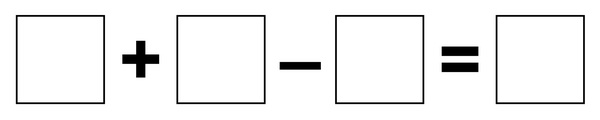
Getting Started
- Spread the symbols out on the table like the picture. Leave room where the boxes are to put in your number tiles.
- The first challenge is to put numbers in the spaces to make a true equation.
- Keep trying until you can do it, then write the solution in your journal.
The Next Challenge
- Find two (2) more ways to do it.
You don't have to find them right now, but you can if you want to.
Or you can come back to this challenge at another time.
- Write the solutions in your journal.
Have fun exploring Truth Tiles 2.
|
 |
The Big Challenge
Now you have found three solutions. Are they really different?
The answer to that depends on how you answer this question.
- Do you think 7 + 2 - 5 = 4 is different from 2 + 7 - 5 = 4?
Write your answer in your journal and give reasons.
- Find one more different solution.
|
 |
There might be more. At this point a mathematician would ask:
- How many different solutions are there?
- How will I know when I have found them all?
Look at the strategies on your working like a mathematician page.
- Which strategy do you think your mathematician might choose to try to find more solutions?
There are at least twelve (12) different solutions.
Find as many as you can and record them.
|
Note: If your school is a member of Maths300, your teacher can provide software that will help you explore Truth Tiles 2.
Digging Deeper
 |
- Blair and Alexander, Year 5, spent about 45 minutes on this problem and discovered a lot. They can give you clues BUT DON'T watch this video until you have found nine (9) solutions by yourself.
When you do watch it you will also notice that they each of them had a page of journal notes about this challenge.
- The numbers in this challenge are consecutive. That means they are one apart - 3, 4, 5, 6, 7.
- What happens if you start at a different number and use five consecutive number in the same way?
|
- What happens if we change the equation to this ... and use the numbers 8, 16, 32, 64?
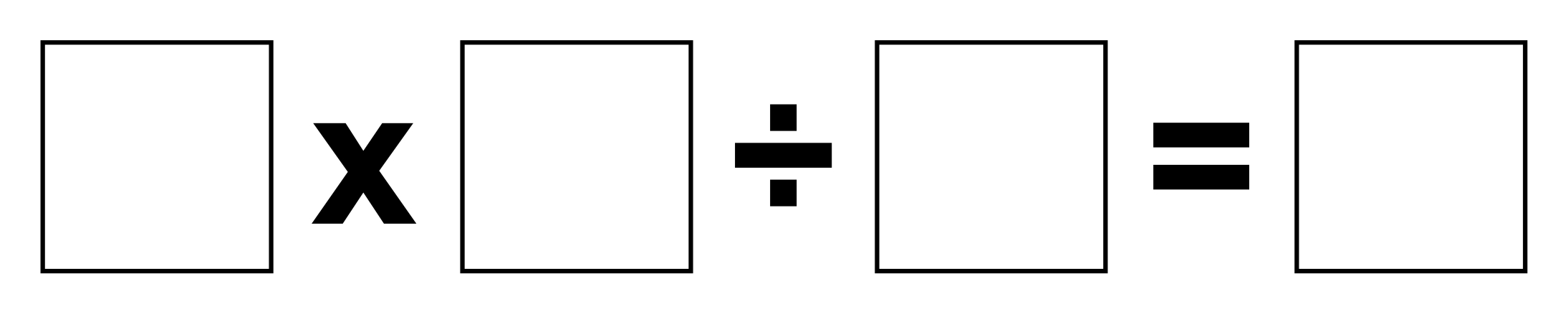
- What happens if we use the numbers 8, 16, 32, 64, 128?
- After you have investigated 4, convert the numbers to powers of 2 and look for connections.
Report on any Digging Deeper investigation in your journal.
Just Before You Finish
Read your Working Like A Mathematician page again and describe how you worked like a mathematician in this activity.

Answers & Discussion
Journals from Ashburton Primary School. These tasks were investigated and recorded in a normal length class lessons.
Click an image to view higher resolution version.
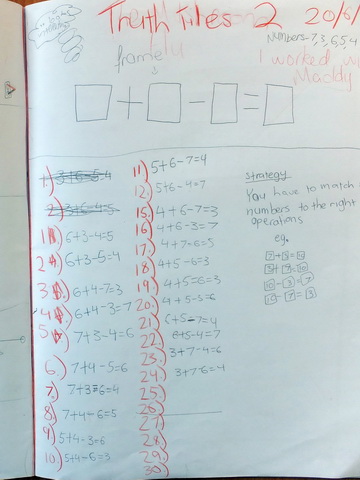
Quin and Maddy, Year 4
 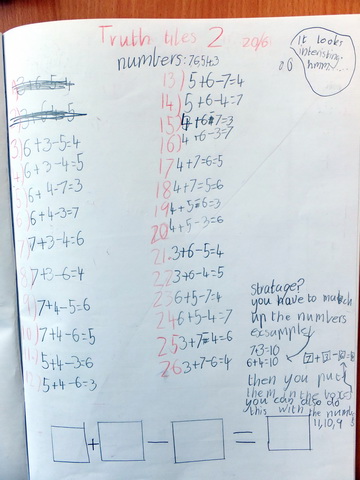
Blair and Alexander, Year 5

These notes were originally written for teachers. We have included them to support parents to help their child learn from Truth Tiles 2.
Send any comments or photos about this activity and we can start a gallery here.

Maths At Home is a division of Mathematics Centre
|








