
Eric The SheepTask 45 ... Years 2 - 12SummaryEric the sheep is lining up to be shorn. He is last in the queue. Each time the shearer takes one sheep from the front of the line, Eric sneaks past two sheep to get closer to the front. If there are 50 sheep in front of Eric to start with, how many will be shorn before Eric gets to the front?
This cameo has a From The Classroom section which contains examples of student work from three levels from schools in three countries, including a PowerPoint presentation from two Year 7 girls. |
Materials
Content
|

IcebergA task is the tip of a learning iceberg. There is always more to a task than is recorded on the card. |

How can you tell if a number is a multiple of 3? or 4? or 5? ... Explore Divisibility Tests. |
Whole Class InvestigationTasks are an invitation for two students to work like a mathematician. Tasks can also be modified to become whole class investigations which model how a mathematician works. |
You have to act this one out. It's the only way to start. Bet you already know who you want to make Eric. 
Teachers' Comments Also:
For more ideas and discussion about this investigation, open a new browser tab (or page) and visit Maths300 Lesson 17, Eric The Sheep, which includes an Investigation Guide and student PowerPoint publications from Year 7. Visit Eric The Sheep in Menu Maths Pack D. |
Is it in Maths With Attitude?Maths With Attitude is a set of hands-on learning kits available from Years 3-10 which structure the use of tasks and whole class investigations into a week by week planner. |
The Eric The Sheep task is an integral part of:
The Eric The Sheep lesson is an integral part of:
|
| In this section you have the opportunity to see how Eric has been explored and reported on in a Year 1 class from the USA, a Year 5 class from the UK and a Year 7 class from a small, remote school in New South Wales. Photos above are from a Year 3 class in Australia. |
Year 1 Accelerated Class, Hammond Westside Primary, Louisiana
Miss Langlois
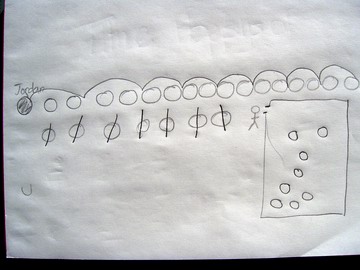
In the first hour with the problem children explored it physically (they became the sheep) then with Poly Plugs. They collected data about some numbers of sheep in front of Jacobi and were fascinated to see that sometimes the number cut (shorn) was the same. In their own way, they recorded what they had done on a journal page. Next day they began the problem again, this time organising their search through the data.
 |
 |

Literacy and numeracy develop hand in hand when students are learning to work like a mathematician. |
Miss Greer's regular Year 1 class, Hammond Westside Primary, Louisiana
The photos below are from their first hour with the problem. Recording on their journal page was a feature too.  |
 |
 |
 |
 |
Year 5, St. Edmund's Junior School, England
| Each week Matthew combines two 'sets' of students for an investigation session of just over an hour. The two Year 5 classes are split for mathematics into three sets (or streams). Matthew takes Sets 1 & 2 in this session.
Sample journal entries from this session are shown below. |

|
|

|
Editor's interpretation of the text we were trying to figure out a problem and was 51 sheep one of the sheep was called eric there were 50 sheep in front of eric waiting to be shawn eric really wanted to be shawn so he skipped 2 sheep every 1 sheep gets shawn So what me and my group did we tried to act it out, first with five people then with 7 but it wasn't working So we decided to get 51 little cubes and we put the cubes in a line and eric at the back then we took a cube away and put eric in front of 2 cubes every time until we got an answer. |
|

|
Editor's interpretation of the text 1. first me and my partner lined up fifty counters not encluding Eric [diagram] hear is a small section of what hapens [diagram] we tried to find out how many sheep were sawn before him. Mathematics Centre News July 2010
G'day Doug,
I was very impressed by the Eric the Sheep stuff added to the cameo from St. Edmund's (June 2010 News). That diagram showing the red/black bar with Eric making his way to the front as the yellow square is terrific. My eyes immediately sprang to the slopes created by the yellow square and the edge of the red section showing the shorn sheep. That obviously provides a new way of finding the solution - looking at the intersection of those two slopes. A very geometric solution where the slopes depend on how many sheep Eric can jump at once and how many shearers are working at once, with the intersection obviously depending also on the size of the queue to start with. That adds another excellent layer to this problem. Wonderful stuff.
Many thanks to St Edmund's. Look forward to using Eric the Sheep again.
Cheers, |
Year 7, Hillston Central School, New South Wales, Australia
Graeme Smyth
Hi Doug,
Attached is a presentation on Eric the Sheep produced by Tiana and Emma, from Year 7 at Hillston Central School. They selected Eric the Sheep as their task to present to Mr Smyth's maths class. The students in this class have really enjoyed the Working Mathematically approach using the Maths With Attitude kits. They did their presentation in Powerpoint, which has been converted to a pdf.Thanks,
Graeme(Editor's Note: Congratulations girls, this is great work.)
- Eric The Sheep by Tiana and Emma
(To view in full screen use Ctrl L.)