Double Staircase

Task 61 ... Years 4 - 10

Summary

Students build staircases of cubes up to a platform and then match the steps down the other side. The challenge is to predict the number of blocks needed to build a double staircase of a given height.

This task is a development of Task 51, Staircase.

Also Staircase is the stimulus investigation for the DIY workshop video Aiming High? Dig Deeper which explores a pedagogy of achieving high aims in mathematics by digging deeper into fertile learning ground such as this task, rather than too quickly moving on to something new. The video highlights teaching craft - for example visual and kinaesthetic learning and journal writing in maths - and uncovers mathematics content from Year 1 to Year 12. Its introductory video Staircase Maths (in less than one minute) will give you an idea of the content (and teaching craft).

 

Materials

  • 18 cubes

Content

  • basic operations with number
  • patterns in tables
  • quadratic algebra including:
    • concept of a variable
    • generalisation
    • substitution
    • solving equations
  • visual representation of symbolic algebra
  • graphical representation of functions
  • concept of proof
Double Staircase

Iceberg

A task is the tip of a learning iceberg. There is always more to a task than is recorded on the card. 		   

The action of building the double staircase is well within the grasp of quite young students. It is also possible for them to work out the total of blocks for a 10-step stair in either pattern on the card, since each can be modelled with square paper or tiles or more blocks, or drawn on graph paper. A calculator might also be a useful tool.

If the focus of the problem was the answer, then this could be all we required. However, if the focus is learning to work like a mathematician, then we need to ask the mathematician's question: Can I check it another way?

This may encourage students to look for connections both visually and numerically. For example, the Question 1 diagram could be thought of as two sets of steps 1 to 3 plus a column of four up the middle.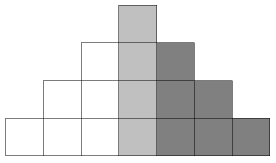

How is it made
The equivalent in a 10-step stair would be two sets of steps 1 to 9 plus a column of 10 up the middle. Then, in adding 1 to 9, students might look for 10s and pair 1 with 9, 2 with 8, 3 with 7, 4 with 6 and realise that the total is therefore 4 tens plus the unpaired 5, which is 45. Doubling this gives 90 and adding the column of 10 makes a total of 100.

More importantly, this process describes how to work out the total of cubes for any height double staircase of the Question 1 variety.

Question 2 might encourage a different way of 'seeing'. They might notice that the towers on the right side of the middle could be used on top of the 'other tower' on the left side to make two towers of 6 to the left of the central tower. That makes it easy to count the 18 in the diagram of Question 2. A 10 step version of this staircase would have towers of 2, 4, 6, ... 18 up each side and a central column of 20. The towers on the right could all be added to a partner on the left to make 9 columns of 20, plus the central one. Again, easier to calculate the 10 lots of 20 and get 200.

Of course, you could also 'swap' approaches between Questions 1 and 2, and there are, no doubt, other ways to look at the staircase patterns.

Additional questions which help explore the iceberg for each diagram are:

  • If I tell you any number of steps, can you tell me the number of blocks I need to build the staircase?
  • If I tell you the number of blocks I have, can you tell me the number of steps in the staircase I build?
  • A mathematician sometimes uses a graph to investigate a problem. Make a graph which links the number of number of steps with the total number of blocks.
  • What would you say to a student who said the dots on the graph should be joined up?
  • What happens if each step in the staircase is 3 blocks higher than the one before it?
  • If I tell you that each step is p blocks higher than the one before it, can you tell me the total of blocks needed to build a staircase with n steps?
Students can also be asked to create their own form of staircase pattern, or other growing pattern.

Whole Class Investigation

Tasks are an invitation for two students to work like a mathematician. Tasks can also be modified to become whole class investigations which model how a mathematician works. 		   

Staircase with Poly Plug To convert this task to a whole class investigation you only need a collection of cubes for each group. Alternatively, if you have Poly Plug you can introduce the investigation in a somewhat quieter, but equally concrete and visual way using the red board.

For more ideas and discussion about this investigation, open a new browser tab (or page) and visit Maths300 Lesson 115, Staircases, which includes an Investigation Guide.

Visit Staircase on Poly Plug & Tasks.

Is it in Maths With Attitude?

Maths With Attitude is a set of hands-on learning kits available from Years 3-10 which structure the use of tasks and whole class investigations into a week by week planner. 		   

The Double Staircase task is an integral part of:

  • MWA Pattern & Algebra Years 9 & 10

The Staircases lesson is an integral part of:

  • MWA Pattern & Algebra Years 5 & 6
  • MWA Pattern & Algebra Years 9 & 10

Green Line
Follow this link to Task Centre Home page.