
Area of a TriangleTask 187 ... Years 4 - 8SummaryStudents play with the pieces in colour sets to make three triangles. Then they measure lengths and choose their own way to calculate the area of the triangles. They don't have to know a formula for calculating triangle area to do this. However, the Challenge encourages them to discover such a rule for themselves. Using the 2cm grid as a check makes it clear that their formula is not dependent on the scale of the measurement, but is actually a property of the triangle.Materials
|
Content
|

IcebergA task is the tip of a learning iceberg. There is always more to a task than is recorded on the card. |
The task is designed to help students discover that the area of a triangle is the same as the area of a related rectangle. Then to discover how the two shapes are related. The sets of pieces are related to suggest that 'it works for all triangles'. Students will notice that for each colour triangle the 'cuts' that have been made to create the pieces are of this form. 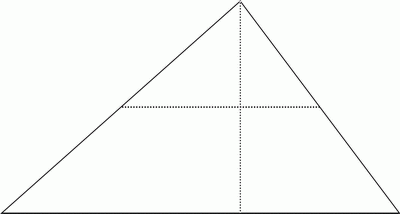
Question 2 asks students to create a table in their books, measure with the grids and record. Answers are shown for the 1cm grid, assuming the base is chosen to be the longest length.
The students can calculate the area in each case, by counting squares. However they might also discover that the small triangle placed on top of the trapezium on the same side shows that the area of each side of the big triangle can be calculated by creating two rectangles.


Each side can be thought of as two rectangles, or as one big rectangle. If the students see the change from triangle to rectangle in this way, then it is not too far away from seeing that consequence is: Area of TriangleOr in symbolic form: A = B x ½Hwhere B is the Base Length and H is the height of the triangle. It is common for students to do the rearrangement asked for in question 4 by messing up the triangle and then trying to make the rectangle 'from scratch'. Encourage them to apply the mathematician's question:
This diagram suggests the usual response...
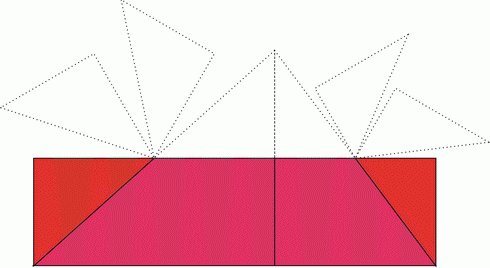
Extensions
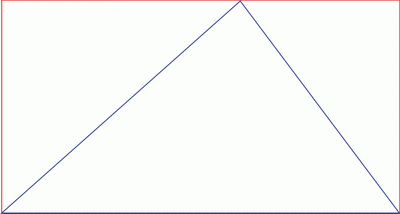
and if we add just one line...
Now we see that the area of the triangle must be half the area of its bounding rectangle. A = ½(B x H)Further extensions might be:
|
Whole Class InvestigationTasks are an invitation for two students to work like a mathematician. Tasks can also be modified to become whole class investigations which model how a mathematician works. |
This lesson takes a little easy preparation. You need to rule four different triangles on four different pieces graph paper and show the construction lines as in the first diagram above. Copies of each are then made on four different coloured pieces of light card. Eight copies of each is plenty for a class. Cut the pieces from each copy and store them separately in an envelope. Now you have a set of jigsaws to start the lesson - and you can use them for class after class. Begin by gathering the students at a central place. Provide two students with one of the coloured wooden sets from the task: This is a simple jigsaw. All four pieces actually make two shapes - a triangle and a rectangle. See if you can make one of them.As they begin, offer a second colour set of wooden pieces to another pair with the same request. Then after a short time pass out the third set. By now all the observers want to have a turn so introduce the envelopes of pieces which you have previously arranged in colour piles on your front table. Okay, your first challenge today is to become confident at making both the rectangle and the triangle for any colour.As this confidence develops gather the class centrally again and ask for a demonstration. You want to introduce the idea of the transformation from one shape to the other, but how you do so will depend on how the making of the two shapes is demonstrated. Your next challenge is to be quite confident that you can transform the triangle into the rectangle, and vice versa, for any colour.As this confidence develops, challenge students to become Master and Robot. The Master keeps their hands behind their back (or sits on them) and instructs the mindless Robot how to construct one of the shapes and transform it. When the students have all tried this briefly discuss and record language which made the instructions clear. Gather the students centrally again and draw attention to the cut lines. Imagine you had a triangle that wasn't pre-cut. What instructions would you give a carpenter to tell them where you wanted the cuts so it could be turned into a rectangle?Discuss and add to the language list as appropriate. Your next challenge is to test your own instructions. Rule two copies of the same triangle on graph paper. On one follow your instructions to show the cut lines. On the other break the rule for one of the lines. Cut both out and see which one makes a rectangle.From students' oral description of how to find the area of a triangle, develop to a written version and then to a formula. Model how to select the key elements of the lesson and prepare a journal entry, then expect students to each prepare their own journal entry with sketches or more careful diagrams. If you are working with electronic journals, a camera will be useful. Continue in the next time period with any of the Extensions suggested above. For more ideas and discussion about this investigation, open a new browser tab (or page) and visit Maths300 Lesson 44, Area of a Triangle, which includes an Investigation Guide that provides a set of triangles like the ones in the task, companion software. an Investigation Guide to support software use and a Classroom Contribution linking the activity to linear algebra and graphs. |
Is it in Maths With Attitude?Maths With Attitude is a set of hands-on learning kits available from Years 3-10 which structure the use of tasks and whole class investigations into a week by week planner. |
The Area of a Triangle task is an integral part of:
The Area of a Triangle lesson is an integral part of:
|