|
Poly Plug Puzzles D
 |
These notes begin with support for turning each menu item into a whole class investigation, then link to the companion Task Cameo, which in turn links to Maths300 (where appropriate).
These investigations involve Number, Computation, Pattern and are suitable for Year Levels: 3 - 8
Discover Menu Maths here.
Order Poly Plug here.
|
|

Menu Maths Packs
|

Submitted by Charles Lovitt.
I like this activity because it is an 'easy to start' game
suitable for Years 2 - 10 which provides a context for:
- practising arithmetic
- applying the process of Working Mathematically
Equipment
- One Poly Plug set for each student, or pair of students.
- Row Points Recording Paper.
|

Visit the Task Cameo for
Task 9, Row Points |
Procedure
I ask the students to take out their yellow/blue board and turn over 13 plugs.
Hold up what you have made. Hey they're nearly all different. Show your picture to three others near you.
After a short time for comparison, I write the following scoring
rules on the board and challenge the students to work out the total
value of their picture.
Scoring
- 5 in a row - 5 points
- 4 in a row - 4 points
- 3 in a row - 3 points
I usually have to make the obvious comment that 'in a row' means
side by side without gaps - and yes, diagonally does count - and no
if it counts as a five it isn't also a four and a three.
Example
This picture scores as shown:
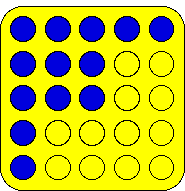
|
Horizontal
5 (Row 1) + 3 (Row 2) + 3 (Row 3) = 11
Vertical
5 (Col 1) + 3 (Col 2) + 3 (Col 3) = 11
Diagonally - falling left
3 (Diag 3) + 4 (Diag 4) = 7
Diagonally - falling right
3 (Leading diagonal) = 3
Total = 32
|
This generates lots of discussion along the lines of What did you
get? and I record a few scores on the board with the names of the
students. After there are half a dozen or so on the board I write
What is the highest possible score? under the heading
Challenge. That sets off another burst of investigation.
It is going to take me too long to check everyone's so
checking has to be your responsibility.
Before a score goes on the board it must be checked by
one other person.
Don't forget to check that there are only 13 plugs
turned over.
As the investigation continues I add more focus questions:
- What is the lowest possible score?
- Are there any scores between the lowest and the highest which
can't be made?
- What scores do symmetric designs get?
There is no need to attempt to complete Row Points in one session - in fact you can't. I use it on a daily basis for a week or so for
mental arithmetic practice. It depends on the students' interest
level. We also keep a display board of results and there is always
blank Poly Plug Paper available for the
students to record their designs.
The best score we have found so far is 40 points. Can anyone beat that? |
|
David Pahl, Wangaratta Primary School, introduced a recording system like this. You can sketch up a similar one or use the one supplied above.

David's class also used a neat strategy to try to find the highest score. They worked their way up using first 3 plugs, then 4, then 5...
What is the maximum score with 3 plugs?
What is the maximum score with 4 plugs?
What is the maximum score with 5 plugs?
and so on to 13. (You can get 6 points with 5 plugs!)
These students also think the top score is 40. Can anyone do better?
|
Variations
- For younger children the game can be played on a 4 x 4 board,
with scoring for only 4 in a row or 3 in a row, by using the red
board and taking out 4 rows of 4 plugs. The yellow plugs are then
placed in the red playing board. Only 9 plugs are used. Seven
holes will therefore be blank.

Equipment
- One red Poly Plug board each
- One paper plate per pair
Problem
Given the number of cookies on a plate and the number of people present to share them, how many cookies will each person receive?
|

Visit the Task Cameo for
Task 19, Cookie Count |
Procedure
- With the class gathered in a circle, or around a central table, present them with a plate of red Poly Plug cookies. Something like 48 is a good number and easy to extract from two boards.
- There are 48 cookies on this plate. There are three people at the party. (Choose three to act the part.) How many cookies would each person get if they were shared equally?
- Ask the class to show/explain at least two ways to work this out. Record the answer and all the methods.
- Put all the cookies back on the plate.
- Before the cookies could be shared, one more person came to the party. Now there are four people. How many cookies would they each get?
- Apply the various methods to work out the answer.
- Put all the cookies back on the plate.
- Before the cookies could be shared, one more person came to the party. Now there are five people. How many cookies would they each get?
- This example introduces the situation of 'left-overs'. Discuss what could be done with these. Depending on the age and experience of the students, you might want to just deal with groups and left-overs. However, it is likely at all levels, that students will suggest interesting ways of sharing these few which will introduce fractions.
Cookie Count is a rich task. It can be visited frequently, and although the structure of the problem remains constant, the challenge in it changes with each different plate of cookies or new number of people at the party. Consequently, once the students understand the structure, it can be threaded into the curriculum for a few minutes a day, two or three times a week over several weeks. Threading is a powerful curriculum model which allows genuine time for the students to construct their own learning. The students do not become bored with the activity and, in fact, find security in the familiar aspects of the challenge.
For this task, each time it is used the instructions are something like:
Make a big pile of cookies on your plate. Count how many there are. Decide how many are coming to your party. Share your cookies and record how many each person will get. Then change your number of people, share again and record. Now do it again.

Equipment
- One Poly Plug set for each pair of students
- One set of counters numbered from 1 - 25
Problem
This well known problem is about a line of sheep waiting to be
shorn. Eric is last in the line and too impatient to wait his turn,
so every time the shearer takes a sheep from the head of the line,
Eric jumps forward 2 sheep. The problem is:
|

Visit the Task Cameo for
Task 45, Eric The Sheep |
Given that you know how many sheep are in the line in front of Eric at the start, how many will be shorn before Eric gets to the head of the line?
Procedure
- The first step in a class approach to this problem is a
kinaesthetic one. Use the children as sheep and try a few numbers
of sheep in front of Eric.
- The second step is a consolidating illustration or two using
the yellow/blue plugs in a place where the whole class can gather
around. (Eric is the blue sheep and the others are yellow). It is
important that every student understands the structure of the
problem before proceeding.
- The third step is to make use of a previously prepared set of
plastic counters numbered from 1 to 25 (say). Hand one counter at
random to each pair and tell them the number on it is the number
of sheep in front of Eric. Ask them to use
yellow/blue Poly Plugs to solve the problem for that number.

Experimenting with the number of sheep in front of Eric
Thorne Grammar, UK, Year 8
- When the partners have solved that problem they bring you the
counter and the actual 'sheep' shorn before Eric.
While they are busy, prepare a line of red boards with plugs in.
As the children return with their counters and shorn sheep build a
graphical representation of the class results as below by popping out
plugs and placing the yellow shorn sheep in their pens.
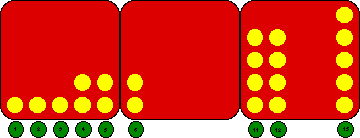 Eric The Sheep results - incomplete
Eric The Sheep results - incomplete
When all results are in, gather the class and consider the graph.
There will be errors, but there will be enough of the pattern for the
students to suggest those data points which need to be checked. Once
checked and corrected the pattern can be used to predict the number
of sheep shorn before Eric reaches the head of the line for 50 or 100
or 1000 sheep in front of him to start with.
Then, there are all the associated what if investigations:
- What if the jumping rule changed?
- What if the number of shearers changed?
|
I have taught this lesson in this way from Year 1 to Year 9 and in
every class the power of the Poly Plug graph, combined with the class
discussion and revision of it, has given every student the confidence
to investigate the 'what ifs', and hypothesise about the
generalisation. In fact, in every class from Year 1 to Year 9 there
has been at least one person who could explain what the "bunches of
three numbers" in the graph has to do with the structure of the
problem.
I also find this approach a fruitful way to highlight the steps of
Working Mathematically, ie: working in context to:
- gather data
- organise data
- seek and see patterns
- communicate and record
- make and test hypotheses
Collecting Class Data
Conway Elementary School
South Carolina, USA, Year 4
|

|

Equipment
- One Poly Plug red board per pair
- Blackbird Sheet - you need to print 12 sheets to get 24 birds
- Royal Garden Sheet - one sheet per pair
Problem
When the pie was open, the birds began to sing ... and the queen was delighted. Every day after that she would look out of her window into the courtyard garden where there were eight feeding platforms arranged like this:
|

Visit the Task Cameo for
Task 62, Four and Twenty Blackbirds
|
And every morning she would see two things:
- a total of 24 birds, and
- 9 birds along each side of three feeding platforms - left/right/top/bottom.
How might the birds have been arranged?
Procedure
- Arrange 8 tables or chairs like the feeding platforms.
- Hand out 24 blackbirds and ask the class to demonstrate a solution to the problem.
- It is likely that they will soon enough come across a solution with 3 birds on each platform.
- Well that's exactly how it looked to the queen, but the next morning the arrangement was different but the 24/9 was still the same.
- Suggest that each pair could use red birds (plugs) and a Royal Garden to look for another arrangement.
- Record the arrangements on the whiteboard as they develop.
- How many solutions are there?
- How do we know when we have found them all?
- Hint: Focus on a particular corner (say top left) and try every possible number in this corner.
- Could the same number of birds be arranged with a different same number along each side, eg: 24/8 or 24/5?
- What happens if the number of birds was different? Could they still be arranged 9 along each side?
- What happens if the king had built a triangle courtyard with 6 feeding platforms in total, one at each corner and one in the middle of each side? Could the blackbirds still be arranged 24/9?

Equipment
- One Poly Plug set per pair
Problem
The task tells us that Bob has a certain number of buttons to share. If he shares them between four people there are two left over. If he shares them between five people, there is one left over. The problem is to find the number of buttons.
Procedure
- Investigate the original problem. There is more than one answer.
- Investigate the pattern in the answers. How does it relate to the original problem?
- Explore What happens if? questions, eg:
- What happens if we change the number of friends?
- What happens if we change the number of left overs?
|

Visit the Task Cameo for
Task 123, Bob's Buttons |

More Poly Plug & Tasks
|











